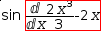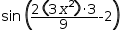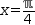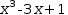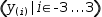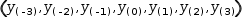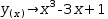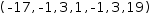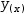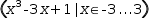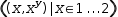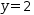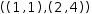3.2.5 Evaluate
While Myron is most often used for algebraic and symbolic
manipulation, sometimes actual numerical values are required. This is
particularly true when a function is plotted. But
evaluation
can also be used as a transformation, and as an alternative to
substitution.
Here is an example with all three kinds of manipulation.
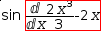 sin .{ⅆ2⋅x^3÷3-2⋅xⅆx}
simplified symbolically is
sin .{ⅆ2⋅x^3÷3-2⋅xⅆx}
simplified symbolically is
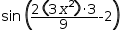 sin (2⋅(3⋅x^2)⋅3÷9-2); simplified algebraically, the latter expression becomes
sin (2⋅(3⋅x^2)⋅3÷9-2); simplified algebraically, the latter expression becomes
 sin (2⋅x^2-2). Provided the workspace contains an equation like
sin (2⋅x^2-2). Provided the workspace contains an equation like
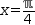 x=ℼ÷4
to define a value for x, and provided the expression containing sin is
active, Evaluate replaces
x=ℼ÷4
to define a value for x, and provided the expression containing sin is
active, Evaluate replaces
 sin (2⋅x^2-2)
with -0.693.
In the last transformation, the value of x is obtained by binding
rather than by substitution and sin is evaluated numerically.
sin (2⋅x^2-2)
with -0.693.
In the last transformation, the value of x is obtained by binding
rather than by substitution and sin is evaluated numerically.
Evaluate examines its subject for operands that are variables and functions. These are
matched with candidates taken from all other expressions in the
workspace; those that are equations with a single variable on either
the right or the left provide variable definitions. There should be
exactly one defining equation or definition in the workspace for each different
variable in the expression being evaluated. The subject is processed
by replacing each variable with its definition, then simplified and
replaced by the resulting value.
The process by which variable references are associated with
definitions is called binding. Evaluation and hence binding are
particularly important when displaying graphs in the plotter. Binding
is explained in more detail in
§9.2.
Consider the polynomial expression
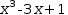 x^3-3⋅x+1. When x=0, the expression evaluates to 1. But when x=2, it evaluates
to 3 and when x=3 it evaluates to 19. To test the expression, add an
equation to the workspace to define a value for the variable x, make
the polynomial active and Evaluate .
x^3-3⋅x+1. When x=0, the expression evaluates to 1. But when x=2, it evaluates
to 3 and when x=3 it evaluates to 19. To test the expression, add an
equation to the workspace to define a value for the variable x, make
the polynomial active and Evaluate .
To evaluate an expression over a range of values, use a
generator. The expression
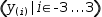 (y(i)|i∈-3, 3)
expands to
(y(i)|i∈-3, 3)
expands to
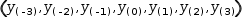 (y(-3), y(-2), y(-1), y(0), y(1), y(2), y(3))
by Distribute . Define a function
(y(-3), y(-2), y(-1), y(0), y(1), y(2), y(3))
by Distribute . Define a function
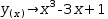 y(x)→x^3-3⋅x+1
by entering
y→x^3-3*x+1. Then Evaluate the expanded generator (or evaluate any individual element). Each
element will be evaluated in turn to produce
y(x)→x^3-3⋅x+1
by entering
y→x^3-3*x+1. Then Evaluate the expanded generator (or evaluate any individual element). Each
element will be evaluated in turn to produce
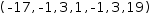 (, -17, -1, 3, 1, -1, 3, 19).
(, -17, -1, 3, 1, -1, 3, 19).
Intermediate expansion can be bypassed by evaluating the generator
directly, given the presence of a function
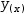 y(x).
y(x).
The use of the function y(x) can be bypassed as well by entering the generator
as
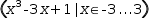 (x^3-3⋅x+1|x∈-3, 3). Distribute and Evaluate on this expression produce the same result, albeit with a
much-expanded intermediate expression.
(x^3-3⋅x+1|x∈-3, 3). Distribute and Evaluate on this expression produce the same result, albeit with a
much-expanded intermediate expression.
At this point, Distribute and Evaluate would appear to be equivalent. However, there is a significant difference. Distribute operates on just the active expression whereas Evaluate takes into account the other expressions in the workspace. In addition, distribute
performs a symbolic expansion of the subject, whereas evaluate performs simplification after
dereferencing bound variables. To see the difference, Distribute applied to 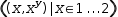 ((x, x^y)|x∈1, 2) results in
((x, x^y)|x∈1, 2) results in
 ((1, 1^y), (2, 2^y)). But Evaluate applied to the same
expression but with
((1, 1^y), (2, 2^y)). But Evaluate applied to the same
expression but with 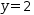 y=2 elsewhere in the workspace
results in
y=2 elsewhere in the workspace
results in 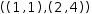 ((1, 1), (2, 4)). In the former case,
((1, 1), (2, 4)). In the former case, 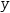 y is unbound
and remains symbolic. In the latter case,
y is unbound
and remains symbolic. In the latter case, 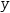 y is bound to 2.
Binding and evaluation are discussed further in §9.2.
y is bound to 2.
Binding and evaluation are discussed further in §9.2.